R Language –Data Structures : Online Course
R Metrics
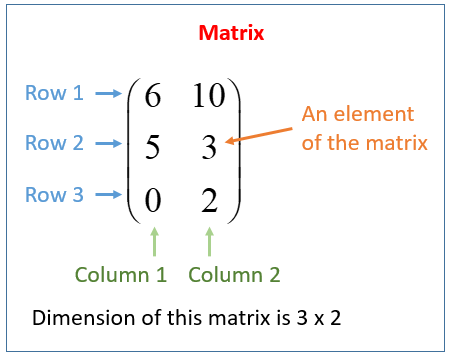
- It is a collection of elements of a two-dimensional rectangular layout. It contain same type of elements.
- In this case, data is arranged in the fixed format (numbers of row and column).
- The entries are the numbers in the matrix known as an element.
- We can perform all arithmetic operation such as (addition, subtraction, multiplication, and division operation).
- The size of a matrix is denoted as ‘n by m’ matrix and is written as m×n, where n = number of rows and m = number of columns.
- A matrix can be created with the
matrix()function.
Example: These are examples of matrices. Here there are 3 rows and 2 columns.
Matrix in R Programming
History of Matrix
The term “matrix” (Latin for “womb”, derived from mater—mother) was coined by James Joseph Sylvester in 1850, who understood a matrix as an object giving rise to a number of determinants today called minors, that is to say, determinants of smaller matrices that are derived from the original one by removing columns and rows. An English mathematician named Cullis was the first to use modern bracket notation for matrices in 1913 and he simultaneously demonstrated the first significant use of the notation A=ai,j to represent a matrix where ai,j refers to the element found in the ith row and the jth column.
Matrix Creation
If you want to create a matrix to required a the matrix() function. The basic syntax for creating a matrix in R is
| matrix(data, nrow, ncol, byrow, dimnames) |
| Following is the description of the parameters used − Sequence: Here the sequence of elements is given. These elements are given according to the matrix() function. nrow : It is the number of rows to be created. ncol : It is the number of columns to be created. byrow: It is a logical clue. If TRUE then the input vector elements are arranged by row. dimname: It is the names assigned to the rows and columns. |
Let’s look at an example of a matrix function. How the matrix function is used to build a matrix and arrange the elements sequentially by row or column.
| Input: Create a matrix from many ways |
| # Create a simple matrix p = matrix(0.5:4.5) p # Create a nrow Parameter in R P1 = matrix(0.5:5.5, nrow = 3) P1 # Create a nrow Parameter in R P2 = matrix(0.5:5.5, ncol=3) P2 #Create a nrow & ncol Parameter in R p3 = matrix(c(1,2,3,4,5,6), nrow = 3, ncol = 2) #Print the matrix p3 |
| Output: |
 |
Name Row & Columns
For example, with the help of ‘dimnames’ parameter, rows and columns have been given different names.
| Input: Use ‘dimnames’ parameter, |
| rownames = c(“row1”, “row2”, “row3”, “row4”) colnames = c(“col1”, “col2”, “col3”) matrix(c(4, 1, 7, 8, 5, 2, 4, 7, 2, 9, 7, 12), nrow = 4, ncol = 3, dimnames = list(rownames, colnames)) |
| Output: |
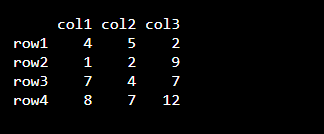 |
Accessing Matrix Elements
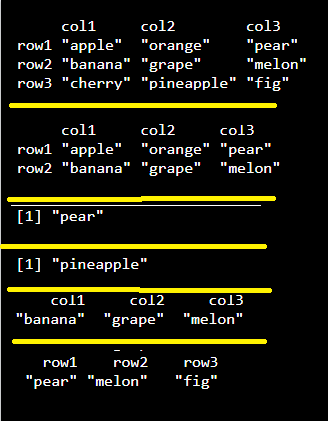
We can also access the elements of the matrix by using the column and row. Elements can be accessed as var[row, column]. Here rows and columns are vectors. We can access by three way, the matrix present on nth row mth column, nth row, or mth column.
Let’s take an example of simple R code.
| Input: Access the matrix present on nth row mth column, nth row, or mth column. |
| #Define the column and row names. rownames = c(“row1”, “row2”, “row3”) colnames = c(“col1”, “col2”, “col3”) #Create the matrix. R <- matrix(c(“apple”, “banana”, “cherry”, “orange”,”grape”, “pineapple”, “pear”, “melon”, “fig”), nrow = 3, ncol = 3, dimnames = list(rownames, colnames)) R #Accessing first and second row print(R[1:2, ]) #Access the element at 3rd column and 1st row. print(R[1,3]) #Access the element at 2nd column and 3th row. print(R[3,2]) #Access only the 2nd row. print(R[2,]) #Access only the 3rd column. print(R[,3]) |
| Output: |
 |
Modification Matrix
We modify the R matrix using various indexing techniques.
| Input: Modify the elements |
| m1 = matrix(c(4, 1, 7, 8, 5, 2, 4, 7, 2, 9, 7, 12), nrow = 4, ncol = 3) m1 #modify a single element m1[2,2] = 10; m1 #modify elements less than 5 m1[m1<5] = 0; m1 |
| Output: |
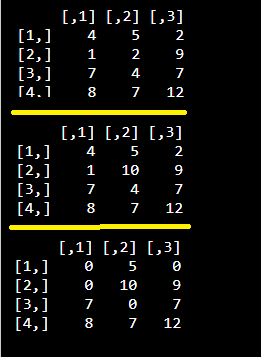 |
Transposing a matrix. We simply use the t() function.
| Input: Transposing a matrix |
| m1 = matrix(c(4, 1, 7, 8, 5, 2, 4, 7, 2, 9, 7, 12), nrow = 4, ncol = 3) m1 #Transposing a matrix t(m1) |
| Output: |
 |
We can add row or column using rbind() and cbind() function. Similarly, it can be removed through reassignment.
Input: Add row or column using rbind() and cbind() function. Removed through reassignmen |
| m1 = matrix(c(4, 1, 7, 8, 5, 2, 4, 7, 2, 9, 7, 12), nrow = 4, ncol = 3) m1 #use cbind function cbind(m1, c(1, 2, 3, 4)) #use rbind function rbind(m1,c(11,22,33)) #remove last row m1 = m1[1:3,];m1 |
| Output: |
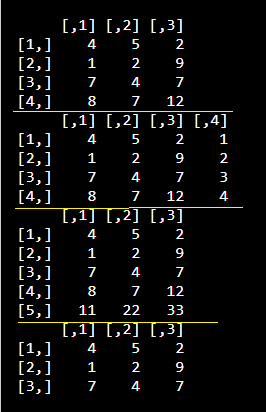 |
Use the dim() function, To find the numbers of rows and columns in a Matrix:
Input: Use the dim() function |
| m1 = matrix(c(“apple”, “banana”, “cherry”, “orange”), nrow = 2, ncol = 2) dim(m1) |
| Output: |
| [1] 2 2 |
Matrix Operation
In R, we can perform several arithmetic operations on matrices like addition, subtraction, multiplication, etc. we can apply this operation when both the matrices have the same dimensions.

| Input: Matrix operation |
| m1 = matrix(c(4, 1, 7, 8, 5, 2, 4, 7, 2, 9, 7, 12), nrow = 4, ncol = 3) m2 = matrix(c(15, 12, 47, 1, 5, 9, 23, 48, 1, 5, 8, 6), nrow = 4, ncol = 3) #Addition m3 = m1 + m2 m3 #Subtraction m4 = m1 – m2 m4 #Multiplication m5 = m1 * m2 m5 #Division m6 = m1 / m2 m6 |
| Output: |
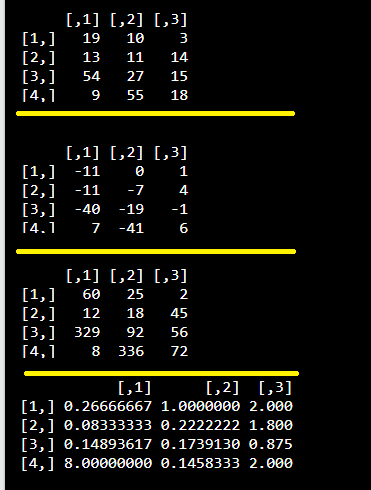 |
R Language: Online Course
आशा करता हूँ, कि यह आर्टिकल आपको पसंद आया होगा तो सोच क्या रहे हैं अभी इसी वक्त इसे अपने दोस्तों के साथ सोशल मीडिया पर Share करें।
Thanking You………………धन्यवाद………………..शुक्रिया………………..मेहरबानी…………………..
Read More
Reference
