Introduction of Number System Notes

In this JEE (Main), Here we are providing you each term that is used in this number system. All the participants should have knowledge about this. It also comes under every competitive exam.

Number System

• The number system is one of the most important topics in Mathematics. 
• A number system is one of the writing systems for categorical numbers.
• It is a mathematical notation range from 0-9 and is termed as digits.
• It provides a unique representation to every term and also represents the arithmetic and algebraic structure.
• The Set is a collection of elements, listed within braces { }.
• In this post, we would explore various kinds of numbers.

Numbers

• In the Decimal number system, there are ten symbols namely 0,1,2,3,4,5,6,7,8 and 9 called digits.
• A number is denoted by a group of these digits called numerals.

Face Value

• The face value of a digit in a numeral is the value of the digit itself.
• For example in 321, the face value of 1 is 1, the face value of 2 is 2, and the face value of 3 is 3.

Place Value

• When a number is written in expanded form, it is known as Place value.
• For Example 512, it is written as 500+ 10+2 and in the word form as five hundred + ten + two.

Natural Numbers

• The natural (or counting) numbers are {1,2,3,4,5,…… N}.
• Which is n > 0 where n is counting number.

Whole Numbers

• The numbers which start from zero (0) are called whole numbers.
• Every natural number is a whole number.
• Which is n ≥ 0 where n is counting number; [0,1,2,3…].

Integers

• Integers are the collection of whole numbers and negative numbers.
• The numbers. …… -5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5, +6, + 7 …. etc.
• Positive Integers – n > 0; [1,2,3…]
• Negative Integers – n < 0; [-1,-2,-3…]
• Non-Positive Integers – n ≤ 0; [0,-1,-2,-3…]
• Non-Negative Integers – n ≥ 0; [0,1,2,3…]
• Even Numbers – n / 2 = 0 where n is counting number; [0,2,4,…]
• Odd Numbers – n / 2 ≠ 0 where n is counting number; [1,3,5,…]

Prime Number

• It is divisible only by itself or 1.
• Set of prime numbers is {2,3,5,7,11,13,17…… }.

Composite Number

• It can be divided exactly by a whole number other than itself.
• The number except 1 and which are not prime.
• A composite number is a number with more than 2 factors.
• Example: Factor 8 are = 1, 2, 4, 8

Co-Primes Numbers 

• Two natural numbers are co-primes if their H.C.F. is 1.
• For example, (2,3), (4,5) are co-primes.

Rational Numbers

• The number can be expressed in the form of p/q.
• Where ‘p’ and ‘q’ are integers and denominator q ≠ 0.
• These may be positive or negative.
• For example, 2/3, 3/5, etc. all are rational numbers.
• Rational numbers that are not integral will have decimal values.
• Two types of Rational Numbers
  1. All decimals which terminate are rational numbers
     • For Example, 8.27 can be written as 827/100.
  2. Decimals that have a repeating pattern after some point are also rationals:
     • For example, 0.0833333….=1/12

Irrational Numbers

• An irrational number is any number that is not rational.
• The numbers which are not written in p/q rational numbers are called irrational numbers.
• An irrational number has endless non-repeating digits to the right of the decimal point.
• Example – √7, √11, π=3.14159265358979… etc.

Real Numbers

• Real numbers comprise any number you can think or use in everyday life.
• Each real number corresponds to exactly one point on the number line, and every point on the number line represents one real number.

• It is the collection of rational and irrational numbers.
• They can be both positive or negative and are denoted by the symbol “R”.
• All the natural numbers, decimals, and fractons fall into this category.

• There are four main properties which include commutative property, associative property, distributive property, inverse property and identity property.
• For any real number a, b and c.

Complex Numbers

• If a and b are real numbers and i is the imaginary unit, then a + bi is called a complex number.
• The value of i = (√-1). 
• If b is 0, the complex number reduces to a which is a purely real number.
• If a is 0, the complex number reduces to bi which is a purely imaginary number.
•  In other words all numbers, real and imaginary, are in the set of complex numbers.
• it can be written in the form

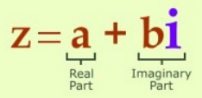
• All numbers can be expressed as complex numbers.

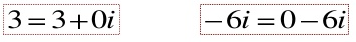
Two complex numbers a + bi and c + di are equal , if a = c and b = d

Note:

1. The set R of real numbers is a proper subset of the Complex Numbers. Hence the Complete Number system is N ⊂ W ⊂ I ⊂ Q ⊂ R ⊂ C.
2. Zero is both purely real as well as purely imaginary but not imaginary.
3. i = (√-1).is called the imaginary unit. Also i² = −1 ; i3 = −i ; i4 = 1 etc.
4. √a√b=√ab only if atleast one of either a or b is non-negative.

Algebraic Operations on Complex Numbers

There are four types of algebraic operations

1. Addition
2. Subtraction
3. Multiplication
4. Division

We know that a complex number is of the form z=a+ib where a and b are real numbers.
Consider two complex numbers z1 = a1 + ib1 and z2 = a2 + ib2

• Addition: z1+z2 =( a1+a2 )+i( b1+b2 )
• Subtraction: z1-z2 =( a1-a2 )+i( b1-b2 )
• Multiplication: z1.z2 = (a1a2 – b1b2) + i(a1b2 +a2 b1)
• Divide: we rationalize the denominator by multiplying and dividing by the conjugate of the complex number. z1/z2 = a1 + ib1/a2 + ib2

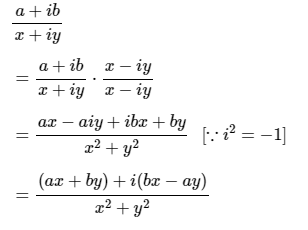
Conjugate Complex

If z = a + ib then its conjugate complex is obtained by changing the sign of its imaginary part & is denoted by z. i.e. z¯ = a − ib.

Equality in Complex Number

Two complex numbers z₁ = a₁ + ib₁ & z₂ = a₂ + ib₂ are equal if and only if their real & imaginary parts coincide.

Here, you have learnt the algebraic operations on complex numbers such as Real Numbers, Complex Numbers, etc. Log onto www.infokhajana.com to cover more topics.

Recommended Reading

JEE (Main) – Number System Notes

References

wikipedia