Most of the time students are confused about the functions of squares, cubes, and their roots, and It can be difficult to identify these numbers without remembering them. So we can discuss this topic by using some example.

In this post, a brief explanation of Squares, Cubes, and Their Roots.

1. Squares & Square Root

Squares

• A square is a number multiplied by itself.
• For Example: 4 = 2 x 2, 9 = 3 x 3 and 16 = 4 x 4.
• When we square a negative number we get a positive result.
• For example: -2 x -2 = 4
• The following is a list of common perfect squares:

02= 0	62= 36
12= 1	72= 49
22= 4	82= 64
32= 9	92= 81
42= 16	102= 100
52= 25	122= 144

Square Roots

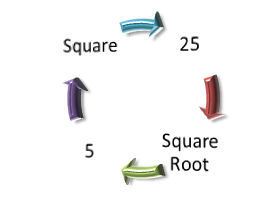
• if a number is a perfect square, then you can find its exact square root.
• A square is a number multiplied by itself. For Example 2*2 = 4.
• The opposite operation to squaring a number is taking the square root.
• For example: Square 6*6 = 36 or 6²= 36 but Square root √36 = 6
• The symbol used to indicate a root is the radical symbo: y = √a
• Since y² = a where ‘a’ is the square of a number ‘y’.
• Every radical expression has three parts…
  1. Radical symbol
  2. Index
  3. Radicand
• Every radical expression has Radical three parts

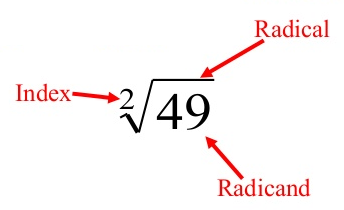
• The index of a square root is always 2.
• In the square root negative numbers is not defined. Because the perfect square cannot be negative. For Example √36 = 6 or -√36 = -6.
• -6 is a also a square root. since -6 * -6 = 36
• Perfect square root does not exist when a number ends with 2, 3, 7 or 8 (in the unit digit).
• If a number ends with 1, 4, 5, 6 or 9 in the unit digit, then the number will have a square root.
• Finding square roots of of numbers that aren’t perfect squares without a calculator
  1. Firstly, find the two perfect square numbers it lies between.
  2. Divide your number by one of those square roots.
  3. So, take the average of the result point 2 and the root.
  4. So use the result of Point 3 to repeat Point 2 and 3 until you have a number that is accurate enough for you.

Example: Calculate the square root of 10 (√10) to 2 decimal places.

1. Find the two perfect square numbers it lies between.
   For Example: √10
   32 = 9 and 42 = 16, so √10 lies between 3 and 4.
2. Divide 10 by 3. 10/3 = 3.33 (you can round off your answer)
3. Average 3.33 and 3. (3.33 + 3)/2 = 3.1667
   Repeat step 2: 10/3.1667 = 3.1579
   Repeat step 3: Average 3.1579 and 3.1667. (3.1579 + 3.1667)/2 = 3.1623
   Try the answer –> Is 3.1623 squared equal to 10: 3.1623 x 3.1623

NUMBER	SQUARE	SQUARE ROOT
1	1	1
2	4	1.414
3	9	1.732
4	16	2
5	25	2.236
6	36	2.449
7	49	2.646
8	64	2.828
9	81	3
10	100	3.162
11	121	3.317
12	144	3.464
13	169	3.606
14	196	3.742
15	225	3.873
16	256	4
17	289	4.123
18	324	4.243
19	361	4.359
20	400	4.472

2. Cubes & Cube Root

Cubes

•  A number (x) is multiplied by itself three times.
• A perfect cube is a number that is the cube of an integer.
• For Example: 8 = 2 x 2 x 2, 27 = 3 x 3 x 3 and 64 = 4 x 4 x 4.
• When we cube a negative number we get a negative result.
• For Example: –8 = –2 x –2 x -2

Cube Root

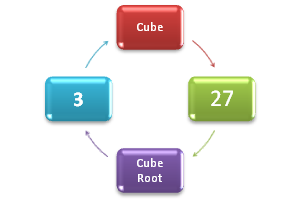
• The inverse operstion of cubing a number is finding the cube root.
• The index of a cube root is always 3.
  • Cube root formula, where y is the cube root of x. ^_∛x=y x³=y. 
• If a number is a perfect cube, then you can find its exact cube root. 
•  A perfect cube is a number that can be written as the cube (raised to third power) of another number.
• If a number is NOT a perfect cube, then you might be able to SIMPLIFY it.

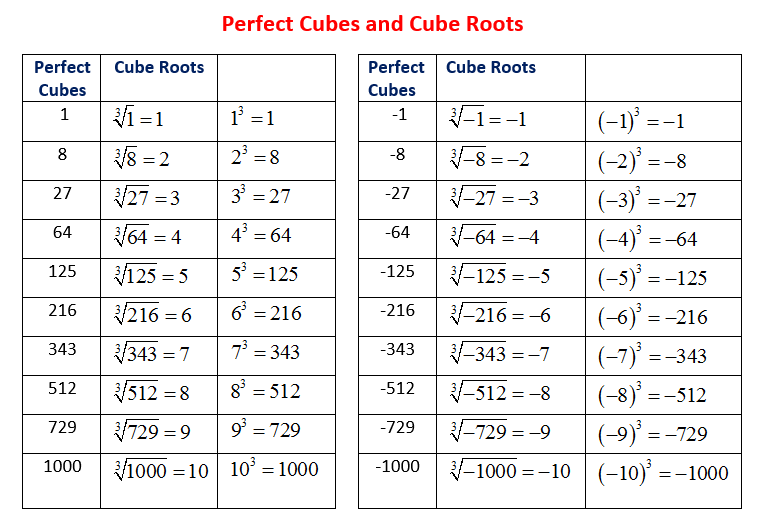
Not all cube roots can be simplified!.

• 30 is not a perfect cube.
• 30 does not have a perfect cube fact.
• For example: _^∛30 cannot be simplified! _^∛30

Here, you have learnt the Squares, Cubes and their roots such as Squares, square root , cubse and cube root. Log onto www.infokhajana.com to cover more topics.Squares Cubes and their roots

Recommended Reading

• JEE (Main) – Number System Notes
• JEE(Main) – Introduction of Number System Notes

References

[1] Weisstein, Eric W. “Square Root.” From MathWorld — A Wolfram Web Resource. Square Root