Automata as a Mathematical Model

A finite state machine is a machine that transitions between states, of which there are finitely many.

For Example

Design a simple finite-state machine (FSM) that models the behavior of a door.

States:

1. Closed State: The door is closed.
2. Open State: The door is open.

Transitions:

• Open Transition: When someone opens a closed door, it transitions from the “Closed” state to the “Open” state.
• Close Transition: When someone closes an open door, it transitions from the “Open” state to the “Closed” state.

Representation:

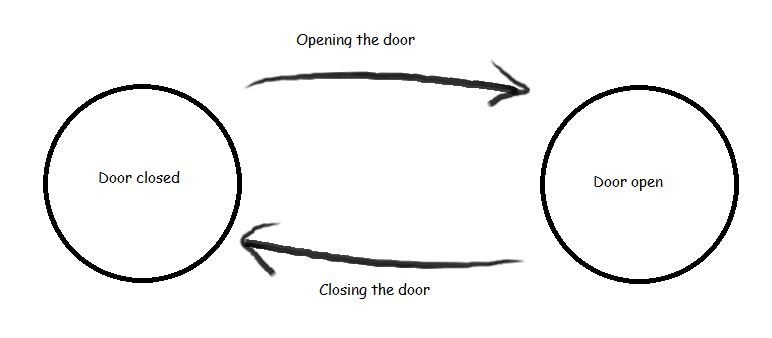
In this representation:

The circles represent the states of the door: “Closed” and “Open”.The arrows indicate the transitions between states based on specific actions (opening or closing the door).The “Closed” state is the initial state, and the “Open” state is a final state.

Behavior:

If the door is initially closed and someone opens it, the door transitions from the “Closed” state to the “Open” state.If the door is in the “Open” state and someone closes it, the door transitions from the “Open” state back to the “Closed” state.

Operating on Different Language Types:

A Finite Automaton (FA) is a versatile mathematical model that can be used to operate on different types of languages. Let’s explore the various types of languages that a Finite Automaton can work with:

1. Regular Languages:
   • Finite Automata are specifically designed to operate on regular languages. Regular languages consist of strings that can be recognized using patterns defined by regular expressions.
   • Regular languages are a subset of formal languages and include languages like simple numeric patterns, keywords in programming languages, and more.
2. Finite Words:
   • Finite Automata can operate on languages composed of finite words, which are sequences of symbols with a definite beginning and end.
   • For example, a Finite Automaton can recognize a language of binary strings where each string consists of a finite number of “0”s and “1”s.
3. Infinite Words:
   • Although Finite Automata are primarily designed for finite languages, certain types of automata, such as Büchi Automata, can also be used to operate on infinite languages or infinite words.
   • Infinite languages include languages like the set of all infinite sequences of “0”s and “1”s that satisfy a specific condition.
4. Trees and Hierarchical Structures:
   • Certain types of automata, such as Tree Automata, are used to operate on languages that involve hierarchical structures like trees.
   • These automata are used in programming language compilers and in parsing languages with complex syntax.
5. Regular Expressions:
   • Although regular expressions are used to describe regular languages, Finite Automata can be built to recognize languages defined by regular expressions.
   • The conversion between regular expressions and Finite Automata is a key concept in automata theory.
6. Input Languages:
   • Finite Automata can work with various types of input languages, including those used in programming, natural languages, and more.
   • For instance, they can be used to validate programming code for syntactic correctness.

Finite and Automaton:

“Finite” in Finite Automaton refers to the fact that both the number of possible states and the number of letters in the alphabet used for input are finite.

“Automaton” signifies that the transition between states is solely determined by the input, without direct human involvement.

Model of Finite Automaton

An automaton is a concept commonly used in the field of automation and production. It refers to a self-operating machine or system that performs certain processes or tasks without direct human intervention. Automata are designed to transform, transmit, and utilize information and materials to achieve specific objectives. They play a crucial role in modern industries, where efficiency, precision, and consistency are paramount. In simple words, we can say It has a set of states and rules for moving from one state to the next, but it is dependent on the input symbol used.

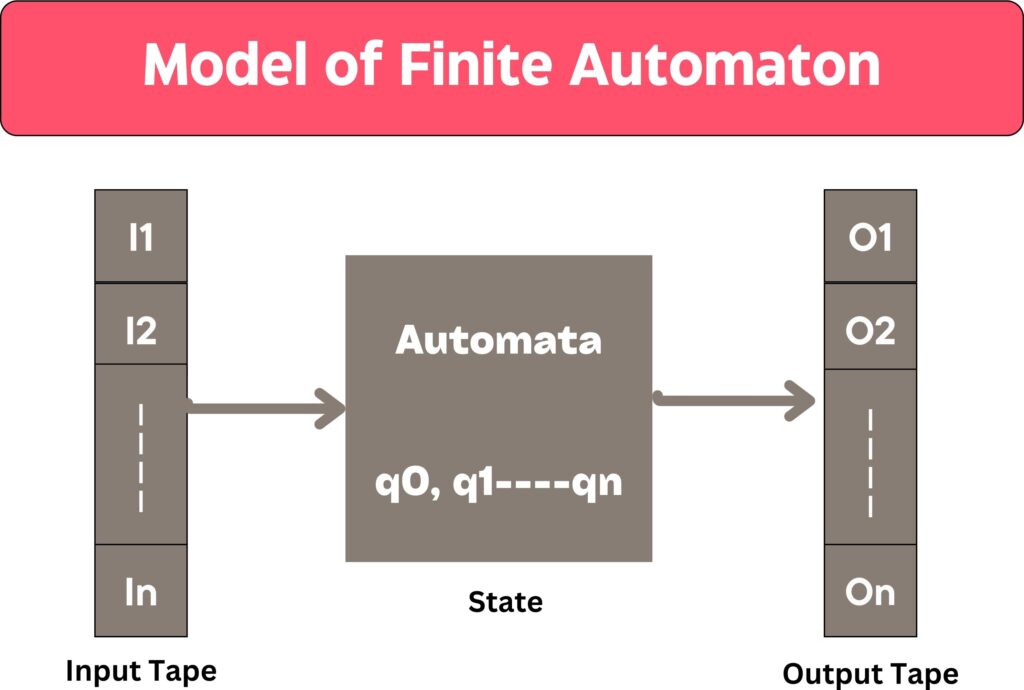
The diagram above depicts the following characteristics of automata:

• Input
• Output
• States of automata
• State relation
• Output relation

Input: Finite Automata takes some input and with the use of this input we can produce some output. The input of the automata is given in the input tape used in the automata. This tape is divided into cells or squares which can hold one symbol at a time.

Output: Finite Automata produce some output with the use of some input.

States of Automata: Automata have finite number of input states. States of Automata like q₀, q₁…q_n.

State Relation: State relations show how automata moves from one state to another state. The next state of the automata at any instant of time is determined by the present state and the input.

Output Relation: The output of finite automata is related to either state only or both the inputs and the states.

Theory of Computation Notes

आशा करता हूँ, कि यह आर्टिकल आपको पसंद आया होगा तो सोच क्या रहे हैं अभी इसी वक्त इसे अपने दोस्तों के साथ सोशल मीडिया पर Share करें।

Thanking You………………धन्यवाद………………..शुक्रिया………………..मेहरबानी…………………..