Byzantine generals problem

“several divisions of the Byzantine army are camped outside an enemy city, each division commanded by its own general. The generals can communicate with one another only by messenger. After observing the
enemy, they must decide upon a common plan of action.”

“Byzantine Generals” metaphor used in the classical paper by Lamport et al. [Lamport et al., 1982]

The paper considered a synchronous system, i.e., a system in which there are known delay bounds for processing and communication.

Byzantine Generals

The problem is given in terms of generals who have surrounded the enemy.

Generals wish to organize a plan of action to attack or to retreat.Each general observes the enemy and communicates his observations to the others.

Unfortunately there are traitors among generals and traitors want to influence this plan to the enemy’s advantage. They may lie about whether they will support a particular plan and what other generals told them.

The game theory analogy behind the Byzantine Generals Problem is that several generals are besieging Byzantium. They have surrounded the city, but they must collectively decide when to attack. If all generals attack at the same time, they will win, but if they attack at different times, they will lose. The generals have no secure communication channels with one another because any messages they send or receive may have been intercepted or deceptively sent by Byzantium’s defenders. How can the generals organize to attack at the same time?

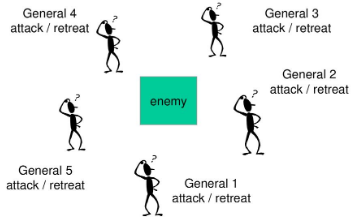
General: either a loyal general or a traitor

Consensus:

A: All loyal generals decide upon the same plan of actions

B: A small number of traitors cannot cause loyal generals to adopt a bad plan

What algorithm for decision making should the generalsuse to reach a Consensus?

What percentage of liars can the algorithm tolerate andstill correctly determine a Consensus?

Assume plan of actions: attack or retreat

• n be the number of generals
• v(i) be the opinion of general i (attack/retreat)
• each general i communicate the value v(i) by messangers to each other general j
• each general final decision obtained by: majority vote among the values v(1), …, v(n)

To satisfy condition A:
every general must apply the majority function to the same values v(1),…,v(n).
But a traitor may send different values to different generals thus generals may receive different values
To satisfy condition B:
for each i, if the i-th general is loyal, then the value he sends must be used by every loyal general as the value v(i)

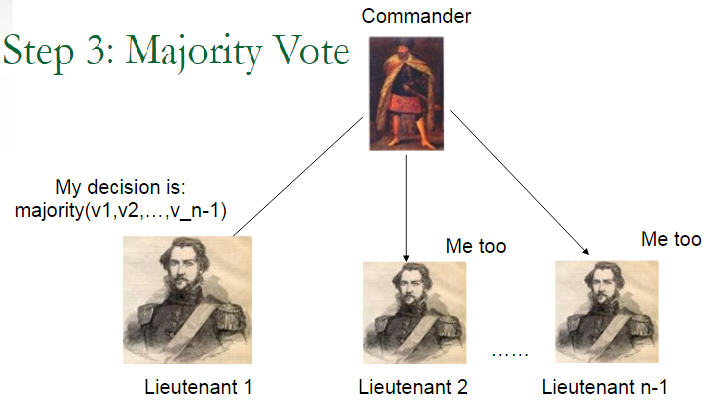
Let us consider the Consensus problem into a simpler situation in which we have: 1 commanding general (C) n-1 lieutenant generals (L1, …, Ln-1)
Consensus:
Interactive Consistency conditions.
IC1: All loyal lieutenant generals obey the same command
IC2: The decision of loyal lieutenants must agree with the commanding general’s order if he is loyal.

Lieutenant generals send messages back and forth among themselves reporting the command received by the Commanding General.

The Byzantine generals problem for 3 loyal generals and 1 traitor.

• The generals announce their troop strengths (in units of 1 thousand soldiers).
• The vectors that each general assembles based on (a)
• The vectors that each general receives in step 3.

The solution to the problem relies on an algorithm that can guarantee that:

1. Using Oral Message

Solution using Oral Message

Solution for more than 3m+1 generals with m traitors

Oral messages:

• Every message that is sent is delivered correctly
• The receiver of a message knows who sent it
• The absence of a message can be detected

Function ‘majority’:

• With the property that if a majority of the values v i equals v, then majority(v 1,…,v n-1 ) equals v.

Order set V i

• Each lieutenant uses it to store orders from others

Algorithm OM(m) can deal with m traitors

• Defined recursively

Base case: OM(0)

• Commander sends messages to Lieutenants
• Each Lieutenant receives and records it. V i ={v 0 :attack}

OM(m)

• Each Lieutenant act as the commander in OM(m-1)
• Send messages to ‘his’ Lieutenants
• Do this recursively attack

What is Byzantine Failure?

 Byzantine Fault is a fault that presents different symptoms to different observers.  a Byzantine Failure is the loss of a system component due to a Byzantine Fault.

So it stands to reason that the objective of a Byzantine Fault Tolerant system is to be able to defend against Byzantine failures.

Therefore, the Byzantine Fault Tolerance model could help in resolving this problem. The generals would need an algorithm that could guarantee the following conditions. 

1. All the loyal generals would act and agree on the same plan of action.
2. The loyal generals of the Byzantine army would not follow a bad plan under the influence of traitor generals.
3. The loyal generals would follow all the rules specified in the algorithm
4. All the loyal generals of the Byzantine army must reach a consensus irrespective of the actions of traitors.
5. Most important of all, the loyal generals should also reach an agreement on a specific and reasonable plan. 

Note that Byzantine faults are the most severe and difficult to deal with. Byzantine fault tolerance has been needed in airplane engine systems, nuclear power plants, and pretty much any system whose actions depend on the results of a large amount of sensors.

Lamport-Shostak-Pease BFT Algorithm

Practical Byzantine Fault Tolerance (pBFT) is a consensus algorithm introduced in the late 90s by Barbara Liskov and Miguel Castro. pBFT was designed to work efficiently in asynchronous (no upper bound on when the response to the request will be received) systems. It is optimized for low overhead time. Its goal was to solve many problems associated with already available Byzantine Fault Tolerance solutions. Application areas include distributed computing and blockchain.

How pBFT works?

pBFT tries to provide a practical Byzantine state machine replication that can work even when malicious nodes are operating in the system.
Nodes in a pBFT enabled distributed system are sequentially ordered with one node being the primary (or the leader node) and others referred to as secondary (or the backup nodes). Note here that any eligible node in the system can become the primary by transitioning from secondary to primary (typically, in the case of a primary node failure). The goal is that all honest nodes help in reaching a consensus regarding the state of the system using the majority rule.

A practical Byzantine Fault Tolerant system can function on the condition that the maximum number of malicious nodes must not be greater than or equal to one-third of all the nodes in the system. As the number of nodes increase, the system becomes more secure.

pBFT consensus rounds are broken into 4 phases (refer with the image below):

·         The client sends a request to the primary(leader) node.

·         The primary(leader) node broadcasts the request to the all the secondary(backup) nodes.

·         The nodes(primary and secondaries) perform the service requested and then send back a reply to the client.

·         The request is served successfully when the client receives ‘m+1’ replies from different nodes in the network with the same result, where m is the maximum number of faulty nodes allowed.

The primary(leader) node is changed during every view(pBFT consensus rounds) and can be substituted by a view change protocol if a predefined quantity of time has passed without the leading node broadcasting a request to the backups(secondary). If needed, a majority of the honest nodes can vote on the legitimacy of the current leading node and replace it with the next leading node in line.

BFT over Asynchronous systems

What’s “asynchronous” Byzantine fault tolerance (ABFT)?

When a decentralized network is Byzantine fault tolerant, it means that the honest members, or nodes, of a network can be guaranteed to agree on the timing and order (consensus) of a set of transactions. Regardless as to whether there are some nodes maliciously trying to prevent that consensus — even if as many as 1/3 of nodes are trying to negatively affect consensus by delaying transactions or otherwise corrupting things. This is the ‘fault tolerance’ of the network, meaning how many nodes can the network tolerate acting maliciously, but still come to an honest consensus.

The ‘asynchronous’ property of Byzantine fault tolerance overcomes a challenge of fault tolerance, which is that of timing. Many forms of Byzantine fault tolerance assume there is a maximum threshold of message latency when coming to a consensus. An asynchronous byzantine fault tolerant (ABFT) network eliminates this assumption and allows for some messages to be lost or indefinitely delayed.

An ABFT network allows for messages to be lost or indefinitely delayed and assumes only that at some point an honest node’s messages will eventually get through. It is much more challenging for an honest node to assess whether another node is not following the rules, if that node’s messages can be indeterminately delayed, but this scenario much better reflects that network reliability in the real world.