Trigonometric identities and equations:

Trigonometry (from Greek trigonon “triangle” + metron “measure”)

• In 1831, Michael Faraday discovers a small electric current when a wire is passed by a magnet.
  • This phenomenon is known as Faraday’s law. This property is used to produce electricity by rotating thousands of wires near large electromagnets.
  • Electric generators supply electricity to most homes at a rate of 60 cycles per second.
  • This rotation causes alternating current in wires and can be modeled by either sine or cosine functions.
  • Equalities that involve trigonometric functions and are true for every single value of the occurring variables.
  •  Identities involving certain functions of one or more angles.

Fundamental Identities

Reciprocal Identities

Defining relations for tangent, cotangent, secant, and cosecant in terms of sine and cosine. The inverse trigonometric functions are partial inverse functions for the trigonometric functions.

tan𝜃 = y /x and cot𝜃 = x/y
therefore, tanθ and cotθ are reciprocals of each other.
The same thing can be said about sinθ and cscθ as well as cscθ and secθ.

The Reciprocal Identities are given as:
sin𝜃 = 1/(csc𝜃)
csc𝜃 = 1/(sin𝜃)
cos𝜃 = 1/(sec𝜃)
sec𝜃 = 1/(cos𝜃)
tan𝜃 = 1/(cot𝜃)
cot𝜃 = 1/(tan𝜃)

Since the product of a number and its reciprocal equals 1, these relations may also be written as:

tanθcotθ=1
cosθsecθ=1
sinθcscθ=1

Quotient Identities

In this diagram, the point (x, y) defines an angle θ at the origin, and the distance from the origin to the point is r units:

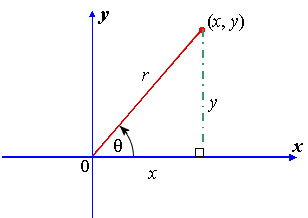
From the diagram, the ratios sin θ and cos θ are defined as:

sinθ = y/r & cosθ = x/r

To find tan θ:

sinθ/cosθ = (y/r)/(x/r) = y/x

But tanθ = y/x

So by transitivity tan𝜃 = sin𝜃/cos𝜃
Since cotθ is the reciprocal of tanθ the quotient can be derived to get cot𝜃 = cos𝜃/sin𝜃

Pythagorean Identities

The basic relationship between the sine and the cosine is the Pythagorean trigonometric identity:
where cos²θ means (cos(θ))² and sin²θ means (sin(θ))².
This can be viewed as a version of the Pythagorean theorem and follows from the equation x² + y² = 1 for the unit circle.

By Pythagorean Theorem, 𝑥² + 𝑦² = 𝑟² .
Dividing both members by r² results to x²/r² + y²/𝑟² = 1.
Since 𝑐𝑜𝑠𝜃 = x/r and 𝑠𝑖𝑛𝜃 = y/r ,
then, cos²θ + sin²θ=1

Dividing both members or 𝒙^𝟐 + 𝒚^𝟐 = 𝒓^𝟐 by x² you get; 1+ tan²𝜃 = sec²𝜃
Dividing both members or 𝒙^𝟐 + 𝒚^𝟐 = 𝒓^𝟐 by y² you get;1+ cot²𝜃 = csc²𝜃

Negative Angle Identities

Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions.

The Negative Angle Identities are given as:
sin(−𝜃) = − sin𝜃
cos(−𝜃) = cos𝜃
tan(−𝜃) = − tan𝜃
csc(−𝜃) = − csc𝜃
sec(−𝜃) = sec𝜃
cot(−𝜃) = − cot𝜃

Reference

wikipedia